The Diamond Kata: a mix of TDD and PBT
[code, haskell]
In this post I show an example of solving a coding kata the TDD way, while writing “property based testing” checks with QuickCheck.
1: Let’s print diamonds
The diamond kata is a well known exercise. Here’s a description copied from codingdojo.org
Given a letter print a diamond starting with ‘A’ with the supplied letter at the widest point.
The program, given the parameters A, C, and E respectively, should print the following patterns:
A A A
B B B B
C C C C
B B D D
A E E
D D
C C
B B
A
I want to rely on two heuristic while writing such a program:
- Test Driven Development:
- Write a test and make sure it is failing
- Write the simplest code that will make the test pass
- Refactor
- Property Based Testing:
- Define properties that should hold about the program’s behavior
- Check the properties using generated data sets the program should be tested against
- Diagnose test failures and fix defects found in the program
Properties Todo List
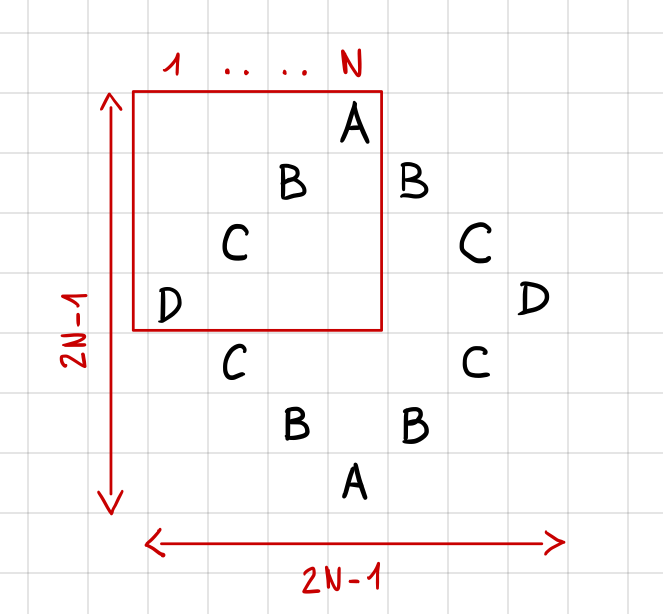
Looking at the diamond examples above, we can find interesting properties about the program’s output.
Given N the position of the (argument) letter in the alphabet,
| The upper left corner of the pattern is filled with a diagonal formed by the letters A,B,C etc. The letter A is in position N (starting from 1), B in position N-1, C, in position N-2, and so on. |
| The pattern has horizontal symmetry, which means that flipping it horizontally yields the initial pattern. |
| The pattern also has vertical symmetry. |
| The height of the diamond is 2N-1. |
| The maximum width of the diamond equals its height, also 2N-1. |
I want to write a program that satisfies these properties, starting with the one that is the easiest, and then adding new properties one after the other.
2: Stating a first property with QuickCheck
Let’s create a test harness and put it in use with a first test. What is the simplest assertion we could hold true about a function diamond which given a letter, yields a pattern of chars in the shape of a diamond?
Well, we could try this:
| For any given letter, the pattern has a length of 2 * N - 1, where N is the position of the letter in the alphabet. |
-- Specs.hs
import Test.QuickCheck
import Diamond
main = do
quickCheck prop_DiamondLengthEquals2NMinus1
prop_DiamondLengthEquals2NMinus1 l =
length (diamond l) == 2 * n - 1
where
n = length ['A'..l]
We can force a test failure with this dummy implementation:
-- Diamond.hs
module Diamond
where
import Data.Char (ord)
diamond _ = []
And sure enough, the test fail:
runhaskell Specs.hs ⏎
*** Failed! Falsified (after 1 test and 1 shrink):
'a'
To make it pass, we can fake the property by creating a list of empty strings having the right length:
-- Diamond.hs
module Diamond
where
import Data.Char (ord)
diamond :: Char -> [String]
diamond l = replicate (2 * n - 1) ""
where n = length ['A'..l]
But our test still fails, and for a different reason:
runhaskell Specs.hs ⏎
*** Failed! Falsified (after 3 tests and 1 shrink):
'1'
This is because length ['A'..'1'] = 0, and replicate used with a negative argument yields an empty list.
The problem is that our test data set is too broad for the function under test, which is expected to work only with capital letters. To solve this, we will use a generator. The function
choose :: System.Random.Random a => (a, a) -> Gen a
will let us generate a char within the legal range for our program, which is 'A' to 'Z'. Then we can combine this generator with the forAll function so that the property get tested only with data from our generator:
-- Specs.hs
import Test.QuickCheck
import Diamond
letter = choose ('A','Z')
main = do
quickCheck (forAll letter prop_DiamondLengthEquals2NMinus1)
prop_DiamondLengthEquals2NMinus1 l =
length (diamond l) == 2 * n - 1
where
n = length ['A'..l]
runhaskell Specs.hs ⏎
+++ OK, passed 100 tests.
Now that the test passes, we can refactor the test code for better clarity during execution:
-- Specs.hs
import Test.QuickCheck
import Diamond
letter = choose ('A','Z')
check s p = do
putStr ("\n" ++ s ++ ": ")
quickCheck p
main = do
check "Diamond length equals 2N-1"
(forAll letter prop_DiamondLengthEquals2NMinus1)
prop_DiamondLengthEquals2NMinus1 l =
length (diamond l) == 2 * n - 1
where
n = length ['A'..l]
And the test results are a bit clearer:
runhaskell Specs.hs ⏎
Diamond length equals 2N-1: +++ OK, passed 100 tests.
3: Checking the diamond’s diagonal
Now we can maybe add some more important properties. Given L, the supplied letter:
| The upper left corner of a the diamond should contain a diagonal formed by the letters A to L. |
“Fake” diagonal
The first property is a bit complicated to write, as it involves comparing each cell in the diagonal to the letters from A to L. For example, if the supplied letter is D, then the cells at positions (i.e. at row and column) {(0,3),(1,2),(2,1),(3,0)} should be filled with letters A, B, C, D.
-- Specs.hs
. . .
main = do
check "Diamond length equals 2N-1"
(forAll letter prop_DiamondLengthEquals2NMinus1)
check "Diamond contains a diagonal with letters A to l"
(forAll letter prop_DiamondContainsDiagonal)
. . .
prop_DiamondContainsDiagonal l =
diagonal (diamond l) == letters
where
diagonal d = [d !! i !! (n-1-i) | i <- [0..n-1]]
n = length letters
letters = ['A'..l]
Of course, the test fails, because the lines in the diamond are empty:
Diamond contains a diagonal with letters A to l:
*** Failed! Exception: 'Prelude.!!: index too large' (after 1 test):
'M'
We can “convince” our test that the property holds by filling the result with series of letters:
- the first N lines with be filled with strings of length N: AAAA.., BBBB.., and so on, until NNNN..
- the next N - 1 lines will be produced the same way, only removing one, so that our first property still holds
module Diamond
where
import Data.Char (ord)
diamond :: Char -> [String]
diamond l = map (replicate n) (letters ++ (tail letters))
where n = length letters
letters = ['A'..l]
Of course, trying this program gives curious results:
ghci Diamonds ⏎
putStr $ unlines $ diamond 'D' ⏎
AAAA
BBBB
CCCC
DDDD
BBBB
CCCC
DDDD
But we are getting closer to our final program.
Spaces
It is true that there is a diagonal formed by the letters A,B,C in the shape above, only it’s not really visible! We should now state something more about the output if we want it to conform to the visual result of a diamond:
| Every cell of the corner that is not part of the diagonal contains a space. |
In other words, given N the position of the supplied letter in the alphabet, for any coordinate {ROW,COL} within the corner, if ROW ≠ N-1-COL then the cell in that position should be a space.
-- Specs.hs
. . .
main = do
check "Diamond length equals 2N-1"
(forAll letter prop_DiamondLengthEquals2NMinus1)
check "Diamond contains a diagonal with letters A to l"
(forAll letter prop_DiamondContainsDiagonal)
check "Diamond contains spaces in non diagonal cells"
(forAll letter prop_DiamondContainsSpaces)
. . .
prop_DiamondContainsSpaces l =
let n = length ['A'..l] in
forAll (choose (0,n-1)) $ \row ->
forAll (choose (0,n-1)) $ \col ->
(row /= (n-1-col)) == (diamond l !! row !! col == ' ')
Now we have to implement this diagonal and stop using fakes.
Fortunately we can use the tails function which produces all the initial segments of a list:
ghci ⏎
import Data.List
tails "***" ⏎
["***","**","*",""]
This, combined with reverse and zipWith, can help us create the desired pattern:
let spacesAfter = reverse (tails " ") ⏎
zipWith (:) "ABCD" spacesAfter ⏎
["A","B ","C ","D "]
let spacesBefore = tails " " ⏎
zipWith (++) spacesBefore $ zipWith (:) "ABCD" spacesAfter ⏎
[" A"," B "," C ","D "]
Let’s put these discoveries into our diamond function:
-- Diamond.hs
module Diamond
where
import Data.Char (ord)
import Data.List (tails)
diamond :: Char -> [String]
diamond l = corner ++ tail corner
where corner = zipWith (++)
spacesBefore
(zipWith (:) letters spacesAfter)
spacesBefore = tails spaces
spacesAfter = reverse spacesBefore
spaces = replicate (n-1) ' '
n = length letters
letters = ['A'..l]
And now all the test pass. Let’s try our code:
ghci Diamonds ⏎
putStr $ unlines $ diamond 'D'
A
B
C
D
B
C
D
We are getting closer to the final result!
4: Horizontal symmetry
Seeing this result helps us find the next property to test:
| The diamond has horizontal symmetry: flipping it should yield the same result |
-- Specs.hs
. . .
main = do
check "Diamond length equals 2N-1"
(forAll letter prop_DiamondLengthEquals2NMinus1)
check "Diamond contains a diagonal with letters A to l"
(forAll letter prop_DiamondContainsDiagonal)
check "Diamond contains spaces in non diagonal cells"
(forAll letter prop_DiamondContainsSpaces)
check "Diamond has horizontal symmetry"
(forAll letter prop_HorizontalSymmetry)
. . .
prop_HorizontalSymmetry l =
diamond l == reverse (diamond l)
The functions tail and reverse are our allied here:
-- Diamond.hs
module Diamond
where
import Data.Char (ord)
import Data.List (tails)
diamond :: Char -> [String]
diamond l = corner ++ tail (reverse corner)
where corner = zipWith (++)
spacesBefore
(zipWith (:) letters spacesAfter)
spacesBefore = tails spaces
spacesAfter = reverse spacesBefore
spaces = replicate (n-1) ' '
n = length letters
letters = ['A'..l]
A look at the result so far:
ghci Diamonds ⏎
putStr $ unlines $ diamond 'D' ⏎
A
B
C
D
C
B
A
5: Vertical symmetry
We are almost done! Here’s a new property:
| The diamond has vertical symmetry: flipping all of its lines should yield the same result |
-- Specs.hs
. . .
main = do
check "Diamond length equals 2N-1"
(forAll letter prop_DiamondLengthEquals2NMinus1)
check "Diamond contains a diagonal with letters A to l"
(forAll letter prop_DiamondContainsDiagonal)
check "Diamond contains spaces in non diagonal cells"
(forAll letter prop_DiamondContainsSpaces)
check "Diamond has horizontal symmetry"
(forAll letter prop_HorizontalSymmetry)
check "Diamond has vertical symmetry"
(forAll letter prop_VerticalSymmetry)
. . .
prop_VerticalSymmetry l =
diamond l == map reverse (diamond l)
To make this test pass, we need to mirror each line of the corner containing the diagonal, i.e. to concatenate it with its reverse:
-- Diamond.hs
module Diamond
where
import Data.Char (ord)
import Data.List (tails)
diamond :: Char -> [String]
diamond l = half ++ tail (reverse half)
where half = map mirror corner
mirror s = s ++ reverse s
corner = zipWith (++)
spacesBefore
(zipWith (:) letters spacesAfter)
spacesBefore = tails spaces
spacesAfter = reverse spacesBefore
spaces = replicate (n-1) ' '
n = length letters
letters = ['A'..l]
We are getting close, but there is still a property that we should add, as is visible in this trial:
ghci Diamonds ⏎
putStr $ unlines $ diamond 'D' ⏎
AA
B B
C C
D D
C C
B B
AA
6: Diamond width
Let’s make sure that:
| The diamond’s width equals 2N-1 where N is the position of the letter. |
-- Specs.hs
. . .
main = do
check "Diamond length equals 2N-1"
(forAll letter prop_DiamondLengthEquals2NMinus1)
check "Diamond contains a diagonal with letters A to l"
(forAll letter prop_DiamondContainsDiagonal)
check "Diamond contains spaces in non diagonal cells"
(forAll letter prop_DiamondContainsSpaces)
check "Diamond has horizontal symmetry"
(forAll letter prop_HorizontalSymmetry)
check "Diamond has vertical symmetry"
(forAll letter prop_VerticalSymmetry)
check "Diamond width equals 2N-1"
(forAll letter prop_DiamondWidthEquals2NMinus1)
. . .
prop_DiamondWidthEquals2NMinus1 l =
maximum (map length (diamond l)) == 2 * n - 1
where
n = length ['A'..l]
Our mirror function should remove the first char of its argument:
-- Diamond.hs
module Diamond
where
import Data.Char (ord)
import Data.List (tails)
diamond :: Char -> [String]
diamond l = half ++ tail (reverse half)
where half = map mirror corner
mirror s = s ++ tail (reverse s)
corner = zipWith (++)
spacesBefore
(zipWith (:) letters spacesAfter)
spacesBefore = tails spaces
spacesAfter = reverse spacesBefore
spaces = replicate (n-1) ' '
n = length letters
letters = ['A'..l]
And some refactoring can occur here, since both horizontal and vertical symmetry can be obtain by mirroring:
-- Diamond.hs
module Diamond
where
import Data.Char (ord)
import Data.List (tails)
diamond :: Char -> [String]
diamond l = mirror (map mirror corner)
where mirror s = s ++ tail (reverse s)
corner = zipWith (++)
spacesBefore
(zipWith (:) letters spacesAfter)
spacesBefore = tails spaces
spacesAfter = reverse spacesBefore
spaces = replicate (n-1) ' '
n = length letters
letters = ['A'..l]
Et voilà! The diamond kata, built the TDD way with quickcheck.
ghci Diamonds ⏎
putStr $ unlines $ diamond 'Z' ⏎
A
B B
C C
D D
E E
F F
G G
H H
I I
J J
K K
L L
M M
N N
O O
P P
Q Q
R R
S S
T T
U U
V V
W W
X X
Y Y
Z Z
Y Y
X X
W W
V V
U U
T T
S S
R R
Q Q
P P
O O
N N
M M
L L
K K
J J
I I
H H
G G
F F
E E
D D
C C
B B
A